离心泵的基本方程式
时间：2012/10/8 来源：浙江扬子江泵业有限公司
离心泵基本方程式从理论上表达了泵的压头与其结构、尺寸、转速及流量等因素之间的关系，它是用于计算离心泵理论压头的基本公式。
离心泵的理论压头是指在理想情况下离心泵可能达到的大压头。所谓理想情况是：1、叶轮为具有无限多叶片的理想叶轮，因此液体质点将完全沿着叶片表面流动，不发生任何环流现象；2、被输送的液体是理想液体，因此无粘性的液体在叶轮内流动时不存在流动阻力。这样，离心泵的理论压头就是具有无限多叶片的离心泵对单位重量理想液体所提供的能量。
液体通过叶轮的流动 基本方程式的推导 基本方程式的讨论
液体通过叶轮的流动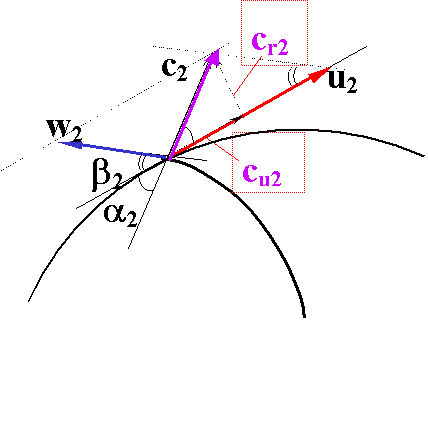
液体质点沿着轴向以绝对速度C进入叶轮，在出口处进行分解得：圆周速度为U2，相对速度W2，两者的合速度即为液体在叶轮出口处的绝对速度C2。
由三个速度所组成的矢量图，称为速度三角形。根据速度三角形可确定各速度间的数量关系。由余弦定律得知：
w12=c12+u12-2c1u1cosα1 （2—1）
w22=c22+u22-2c2u2cosα2 （2—1a）
离心泵基本方程式可由离心力作功推导，也可根据动量理论求得。
△M=QTρ（c2R2cosα2-c1R1cosα1）
ω△M=HT∞QTρg
★∴HT∞ =（u2c2cosα2-u1c1cosα1）/g (2—5)
此式即为离心泵基本方程。在离心泵设计中，使α1=900，则cosα1=0，可提高理论压头。
将（2-5）作进一步的变换可以说明离心泵的工作原理，（2-1，2-1a）代入（2-5）：
★HT∞ =（u22-u12）/2g+（w12-w22）/2g+（c22-c12）/2g (2—5)
（u22-u12）/2g——液体随叶轮旋转增加的静压头；
（w12-w22）/2g——流道扩大，绝对速度转换的静压头；
（c22-c12）/2g——动压头（有部分在泵壳转为静压头）。
理论流量可表示为在叶轮出口处的液体径向速度和叶片末端圆周出口面积之乘积，即QT=cr2πD2b2 （2—6）
由出口的速度三角形：
（cu2=）c2cosα2=u2-cr2ctgβ2
再由HT∞ =（u2c2cosα2-u1c1cosα1）/g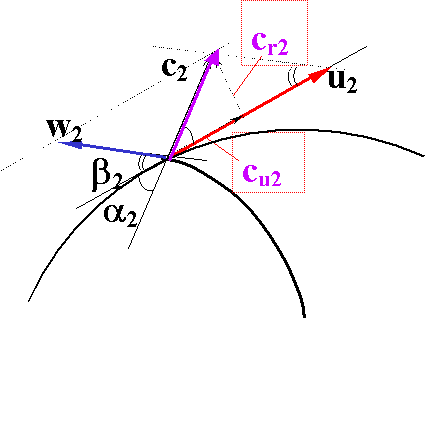 
提高理论压头：
HT∞ =（u2c2cosα2）/g （α1=90o）
合并以上三式得：
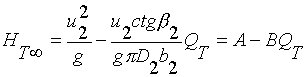其中：u2=πD2n/60
上式表示离心泵的理论压头HT与理论流量QT、叶轮的转速n和直径D2、叶片的几何形状之间的关系。下面分别讨论各项影响因素。
1、叶轮的转速和直径
当QT、β2、b2、一定时，n↑D2↑ 则：HT∞↑
2、叶片的几何形状
根据流动角β2的大小，可将叶片形状分为后弯、径向和前弯叶片
三种：
|
叶片 |
条件 | 形状 |
备注 |
| 前弯叶片 | β2>900 ctgβ2<0 HT∞>(u2)2/g |
 |
产生的理论压头大 |
| 径向叶片 | β2=900 ctgβ2=0 HT∞=(u2)2/g |
 |
|
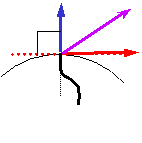| 后弯叶片 | β2<900 ctgβ2>0 HT∞<(u2)2/g |
 |
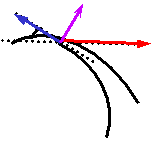实际上离心泵多采用的一种叶片 |
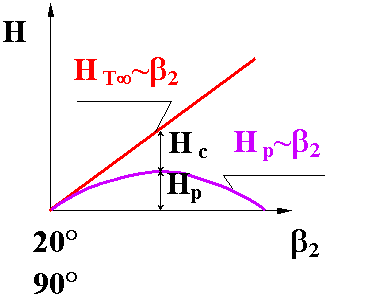左图为不同β2下静压头Hp和动压头Hc的比例关系。
其中后弯叶片产生的静能/动能比大，能损小。
所以，为提高离心泵的经济指标，通常离心泵采用后弯叶片
3、理论流量
若离心泵的几何尺寸（D2、b2、β2）和转速（n）一定，则：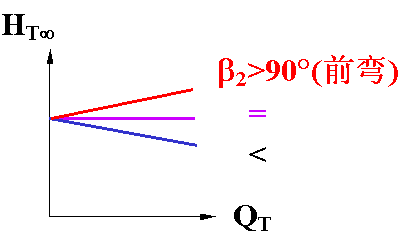
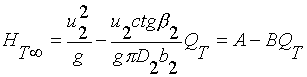上图表示了HT∞与QT的线性关系，斜率随着β2变，后弯叶片的HT∞--QT的关系曲线称为离心泵的“理论特性曲线”。
实际生产中，A、叶片时有限的，液体流动时会产生与流动方向不一致的“轴向涡流”→H↓；B、实际流体与叶轮、泵壳等流道上的元件间不可避免的能量损失→H↓；C、泵内各种泄漏损失：高压液体的部分回流、平衡孔的回流液、轴封处的泄漏→Q↓。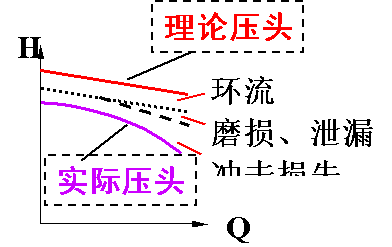
于是，离心泵的H--Q线常须通过实验来测定。
还应指出，离心泵的压头H与所输送液体的密度ρ无关，但泵出口处液体的压强与密度ρ成正比。为了清楚地了解离心泵的工作情况，往往在泵的吸入口附近安装一个真空表（有时为压力表）；在排出管的调节阀前安装一个压力表。当调节流量是，测压表的指针随之变化。
感谢您访问我们扬子江泵业的网站www.yzj.cc，如有任何水泵疑问我们一定会尽心尽力为您提供优质的服务。
- 下一篇：喷淋泵的工作原理
- 上一篇：单相潜水泵特点及用途
